A quick overview of the mathsconf14 sessions I went to, with my takeaways and links to the blogs of the speakers, who obviously put it much more eloquently than I can, which is why they were presenting!
First though, a little aside about the night before and the friendships formed over the conference. I started going to mathsconfs by myself, and still do. However, I do not feel like I am by myself when I attend as the good folks of mathsconfs are always very welcoming, and I hope I am now passing that on to new folks. As well as wonderful CPD, mathsconf brings together maths teachers who are passionate about their subject and want to talk about it (amongst other things of course!).
Andrew Taylor delivered another informative key note message at the start of the day, and following some speed dating, during which @AMercerMaths shared with me the Teach Like a Champion mat. I’m part way through TLAC 2.0, and have listened to @MrBartonMaths podcast with Doug Lemov and it is always good to be reminded of the many ideas that Doug has seen and written about.
Workshop 1: Naveen @naveenfrizvi – Engelmann Insights: Structuring Teaching for the Weakest Pupils
As I have the pleasure of teaching 2 nurture groups (and 1 almost nurture group) this year, it was a no brainer for me to go to Naveen’s workshop. I’ve heard Naveen present a few times before, and I really like the thought she puts into the maths pedagogy she presents about. This presentation was about her experience using Engelmann’s book Connecting Maths Concepts, using an example of teaching fractions and how Engelmann breaks it down into small, well structured and sequence steps. The books are targetted for intervention groups, which is how Naveen has used it, but I did ask Naveen if the ideas could be used for whole class teaching of weaker students, to which she did say that the principles could be applied to whole class teaching. Naveen is blogging about her presentation here.
My takeaways:
Connecting Maths Concepts uses scripts (remember it’s for an intervention group), but even without a script I should think more about the language I use and be careful about not using redundant language. Say more in less words.
“Future learning never contradicts prior learning”. My immediate thought of this was about division with remainders. For example, when first learning 5÷4, a student may be taught to write 1 r1. Then later on, they are taught not to write this any more, but 1 1/4. It may depend on sequencing of teaching, but why not teach 1 1/4 to begin with?

Pre-empt future misconceptions by thinking carefully about how you introduce earlier parts of the topics, as in the very first example of writing a fraction of a shape. Use more than one whole unit to emphasise the denominator is the number of parts in one unit.
Show that equivalent fractions is actually multiplying by 1, but replacing the 1 with, for example, 3/3 instead of using arrows!
Workshop 2: Danielle @piximaths – Scaffolding in Maths Education
Anybody who looks online for maths resources should already know about @piximaths and her wonderful collection of resources that she’s built up over the years. Danielle has also blogged about mathsconf14 here, and has included her slides for her presentation. It was good to have discussions on the table on how we would scaffold certain topics. We went off on a tangent from the directed topic (adding fractions), but that just gave us more insights. It was interesting how between us we thought of different ways to scaffold.
My takeaways:
 Danielle shared Alibali’s ideas for scaffolding, which reminds me not to always use the same method.
Danielle shared Alibali’s ideas for scaffolding, which reminds me not to always use the same method.
The most important part of scaffolding is to take it away.
To think about whole class scaffolding vs individual scaffolding – i.e. 1 worksheet which begins scaffolded and students can start at the appropriate point vs 3 worksheets with the same questions, where 1 is very scaffolded, then second has some scaffolding and the third is without scaffold (and the first two gradually take the scaffold away).
To further review the difference between scaffolding and differentiating by time.
Tweet-up

The wonderful @MrMattock had got a few of us organised to run some puzzles and games at lunch time. I kind of overran eating my lunch and chatting with Jo and Craig, but I finally arrived with the puzzle I first discovered on @mathequalslove blog here, Petals Around A Rose. I’m sorry to Jess and @sheena2907, amongst others, who I annoyed with it, using it as an example of needing resilience. Unfortunately it meant I didn’t get to see other Tweet-up puzzles, but it was lovely chatting to new people.
Workshop 3: Jemma @jemmaths – Building Effective Learning Strategies into a Maths Curriculum
I chose to go to Jemma’s workshop as this is what maths pedagogy is all about to me – using the most effective learning strategies. In this session, Jemma elaborated on the article that she wrote for Learning Scientists here, which explains how she is embedding the six strategies of effective learning from the Learning Scientists into her maths curriculum at her school.
My takeaways:
Spaced practice: I love using Numeracy Ninjas every lesson for my Year 9 nurture group. They’re all building up stickers on the front of their books and I’ve been really impressed with the progress some have made. I also use BBQs (Bread and Butter Quizzes) for my year 10 and 11 groups, which means it’s never too long between returning to previous topics.
Interleaving: This is definitely an area I want to work on – bringing previous learning into next topics. At the moment this only occurs on an ad-hoc basis, but it would be far more ideal if previous learning was planned into new topics. Jemma describes beautifully how it works in her curriculum, which has the advantage that she designed the curriculum so that she could interleave.
Retrieval Practice: This is something I’ve started working on recently. The BBQs, which I’ve been using for a few years now can be seen as a type of retrieval practice as well as spaced practice. However, this term I’ve introduced weekly quizzes for my year 7 and year 9 groups. They have a homework with “last week, last topic, a previous topic” questions, which we self assess and review in lesson every Thursday. On the Friday they then do a quiz, with same questions, different numbers, and an added “this week” section. They must attempt if first of all without their books, but after about 10 minutes, if they have got to the end and have gaps, I allow them to look in their books. I can definitely see improvements for some students, but we’re still early in its infancy, and I know for some I need to help develop their resilience and pride in their work as well.
Elaboration: As Jemma says, “sweat the small stuff”!
Concrete Examples: A given!
Dual Coding: Another area I want to read more into. I’m aware that it’s representing with images or diagrams and not using additional text, but also that an image or diagram in conjunction with the spoken work is processed better than text that is read out. It is definitely an area I need to develop.
Workshop 4: Craig @MrBartonMaths – How I Wish I Taught Maths, 2 months on..
 Initially I wasn’t going to go to Craig’s workshop. Not that I didn’t want to hear what he said, but more that I had already vacuumed up his book in a weekend of frenzied reading, and have listened to many of his podcasts with the experts from which Craig’s reading into the research had originated. How glad I am I changed my mind! Craig is a fantastic speaker and his depth of thought into maths teaching is inspiring. I have no problem in recommending any maths teacher, new or experienced, read Craig’s book. Craig chose 5 areas of his book to talk about, elaborating on what he wrote in the book, and adding some special little nuggets in for us.
Initially I wasn’t going to go to Craig’s workshop. Not that I didn’t want to hear what he said, but more that I had already vacuumed up his book in a weekend of frenzied reading, and have listened to many of his podcasts with the experts from which Craig’s reading into the research had originated. How glad I am I changed my mind! Craig is a fantastic speaker and his depth of thought into maths teaching is inspiring. I have no problem in recommending any maths teacher, new or experienced, read Craig’s book. Craig chose 5 areas of his book to talk about, elaborating on what he wrote in the book, and adding some special little nuggets in for us.
My takeaways:
I’ve got to try some goal free problems, especially with my year 11. Get a problem, take away the actual question part (the goal) and replace it with “what can you find out”.
I’ve already started using example pair problems, but what I want to improve is the “show-call” part of the “Your Turn”, using my visualiser to show student responses and discuss the best parts of them and if there can be improvements.
 Intelligent practice is something else I am striving towards. At the moment, I attempt it rarely, but it is something that can become a powerful tool in students initial learning and understanding of a concept. Craig’s example with product of prime factors blew my mind! I thought it was genius how the questions develop so students can start to expect a certain answer, and then check it with their learning. And then every now and again a cognitive shock is thrown in when the answer isn’t what they expect and they look to see why, involving the hypercorrection affect (learning is more powerful when you are wrong about something you thought was correct).
Intelligent practice is something else I am striving towards. At the moment, I attempt it rarely, but it is something that can become a powerful tool in students initial learning and understanding of a concept. Craig’s example with product of prime factors blew my mind! I thought it was genius how the questions develop so students can start to expect a certain answer, and then check it with their learning. And then every now and again a cognitive shock is thrown in when the answer isn’t what they expect and they look to see why, involving the hypercorrection affect (learning is more powerful when you are wrong about something you thought was correct).
Purposeful practice is another area that I’m trying to develop. This is for when students have learned the concept, but need more practice, and is trying to get away from just having questions to practice and towards practicing with a purpose (surprisingly!). I have already started looking at @colinfoster77 etudes which are ideal for purposeful practice. This was where Craig introduced the first of his golden nuggets, as he announced that he had collated and added to his collection of venn diagram problems, which are great for purposeful practice, on a new website www.mathsvenns.com, and I’m really pleased to say it came with a lot of venn puns!
 Same structure, different deep problems (SSDD problems) were something else Craig introduced in his book and has since developed. These are problems which look the same, or are in the same context, but have different mathematical requirements for them, as on the example shown (this is one of mine!!). In this case they are different types of percentage questions, but the mathematical concepts in each question does not have to be related. Time for Craig’s second golden nugget – he has set up another website www.ssddproblems.com, to collate and share these problems. All he asks is that you submit one (or more) of your own, based on a shape, an image or a context.
Same structure, different deep problems (SSDD problems) were something else Craig introduced in his book and has since developed. These are problems which look the same, or are in the same context, but have different mathematical requirements for them, as on the example shown (this is one of mine!!). In this case they are different types of percentage questions, but the mathematical concepts in each question does not have to be related. Time for Craig’s second golden nugget – he has set up another website www.ssddproblems.com, to collate and share these problems. All he asks is that you submit one (or more) of your own, based on a shape, an image or a context.
And finally…
From the bottom of my pedagogical maths teaching heart, I cannot thank the presenters enough for all that they do sharing their experience and response to research, and of course to Mark McCourt, @LaSalleEd for bringing it altogether and enabling such an event.
On a personal note, it was wonderful to meet up yet again with some twitter and mathsconf acquaintances who I hope I can now call friends. And it was in discussion with these friends that I am starting to believe in myself and my pedagogy again after recently experiencing feedback from a 15 minute observation which left me crushed and devastated when told what I was doing was “wrong”, despite (but not being allowed to) being able to justify why I did each part. Speaking with far more experienced maths teachers than me has given me my confidence back that I can keep developing my practice in order to help student learn maths in the most effective and long lasting manner that research is currently pointing towards. I know I still have a lot to learn and to implement and I hope I can continue doing this to impact positively on my students.







 Another Saturday in June and another education conference, and another gorgeous setting, this time in Rugby. The stairs are important – they’re the two spiral flights we went up and down to get to the maths room. Most times when I go to a conference, my exercise is considerably lacking on that day, but ResearchEd Rugby even managed to account for step rate too! There was a good maths line up, which is where I spent most of the day, but I did venture out to a couple of other sessions, so I’ll start with the one I was most excited to go to, and come onto the maths afterwards. (As always, apologies if I’ve misinterpreted anything, or just got it wrong).
Another Saturday in June and another education conference, and another gorgeous setting, this time in Rugby. The stairs are important – they’re the two spiral flights we went up and down to get to the maths room. Most times when I go to a conference, my exercise is considerably lacking on that day, but ResearchEd Rugby even managed to account for step rate too! There was a good maths line up, which is where I spent most of the day, but I did venture out to a couple of other sessions, so I’ll start with the one I was most excited to go to, and come onto the maths afterwards. (As always, apologies if I’ve misinterpreted anything, or just got it wrong).


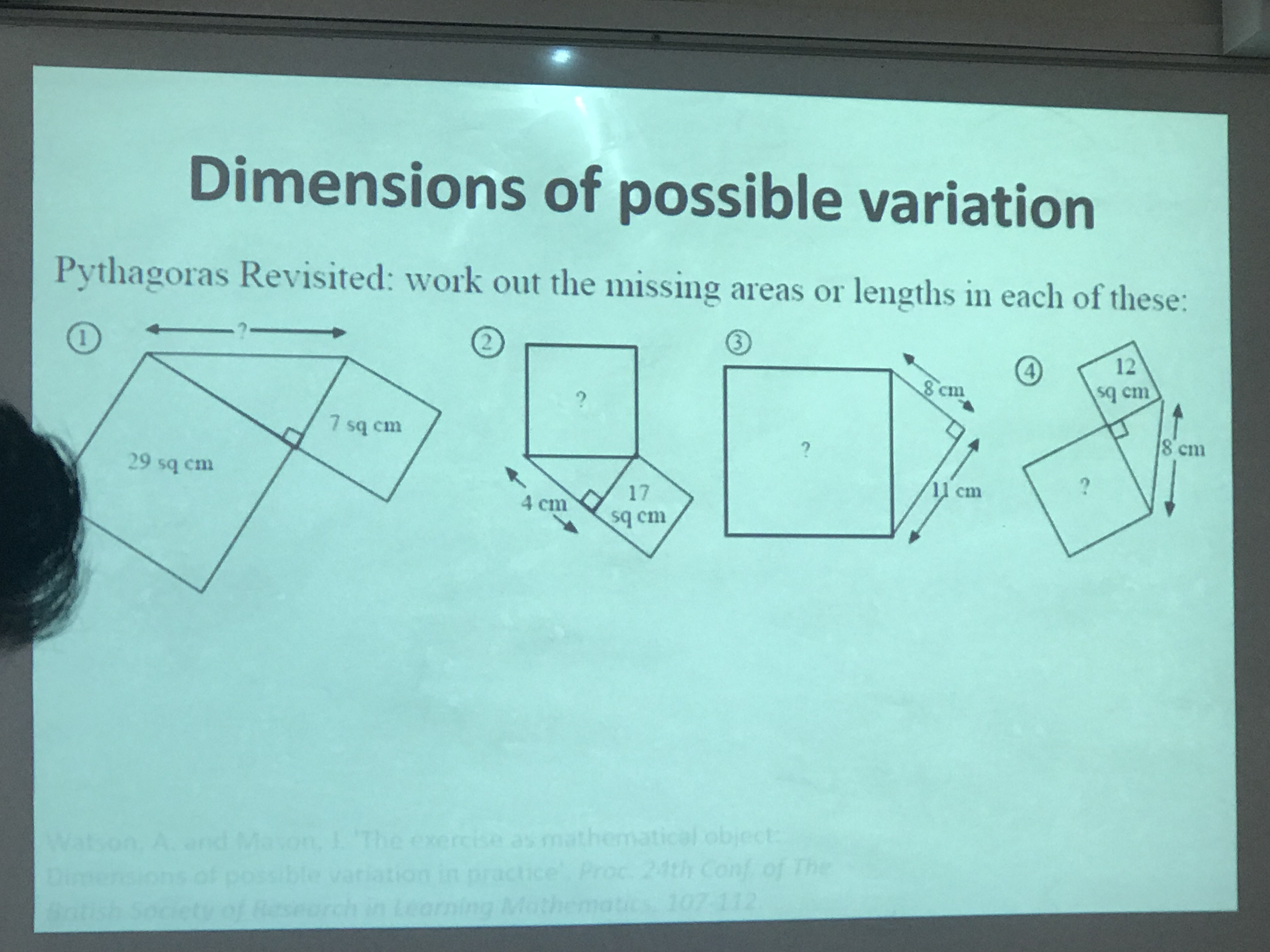 When presenting some of the possible ideas of practice tasks, Tom’s purpose was to find tasks that can develop fluency, but also allow for mathematical reasoning. He indicated that the research said that these tasks were as effective as straight forward exercise tasks, but they can be more motivating and enriching.
When presenting some of the possible ideas of practice tasks, Tom’s purpose was to find tasks that can develop fluency, but also allow for mathematical reasoning. He indicated that the research said that these tasks were as effective as straight forward exercise tasks, but they can be more motivating and enriching.  We had a go at a few of these; this Pythagoras task adds another dimension to your normal “square, square, add or subtract, square root” type questions, and the multiplication task (which I’ve used before) gave us chance to explore some reasoning.
We had a go at a few of these; this Pythagoras task adds another dimension to your normal “square, square, add or subtract, square root” type questions, and the multiplication task (which I’ve used before) gave us chance to explore some reasoning.
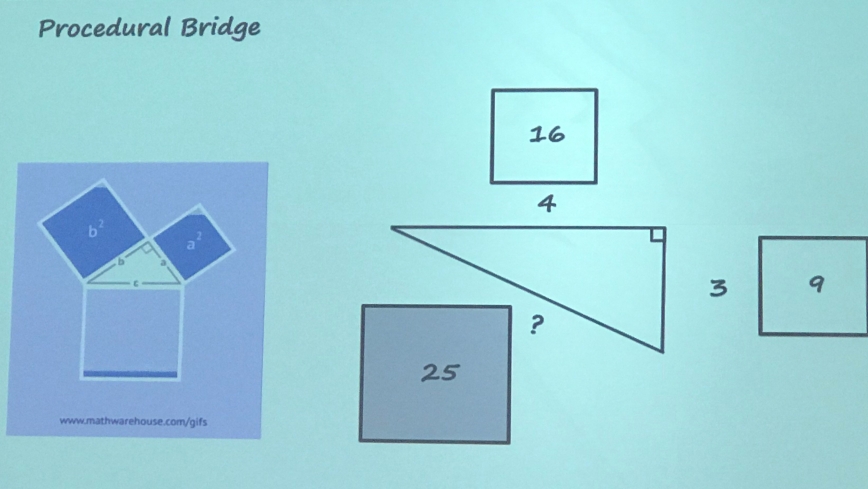 The next idea was a game changer for Andy, and I love it! I wouldn’t even call it a procedure, but more making Pythagoras’ Theorem a bit more concrete, rather than the abstract algebra workings. I (and I’m sure many do) introduce Pythagoras looking at the square of the sides of the right angled triangle. Well why not draw squares next to each side and put the square value in?
The next idea was a game changer for Andy, and I love it! I wouldn’t even call it a procedure, but more making Pythagoras’ Theorem a bit more concrete, rather than the abstract algebra workings. I (and I’m sure many do) introduce Pythagoras looking at the square of the sides of the right angled triangle. Well why not draw squares next to each side and put the square value in? The DM method is basically a procedure to use for any maths that can be set up in proportional grids From ratios, to map scales, equivalent fractions to even inverse proportion.
The DM method is basically a procedure to use for any maths that can be set up in proportional grids From ratios, to map scales, equivalent fractions to even inverse proportion.
 She looked at some of the definitions that have been given about problem solving and shared what what I thought was a great summary: challenging for individual learners; involves a strategy for solving that is not immediate or obvious and involve independent thought and creativity. Problem solving is another of my projects in our department, as we develop our SHAPED problem solving (taking the SHAPED genius of my HOD to implement it effectively to improve problem solving – hopefully more on this to come).
She looked at some of the definitions that have been given about problem solving and shared what what I thought was a great summary: challenging for individual learners; involves a strategy for solving that is not immediate or obvious and involve independent thought and creativity. Problem solving is another of my projects in our department, as we develop our SHAPED problem solving (taking the SHAPED genius of my HOD to implement it effectively to improve problem solving – hopefully more on this to come).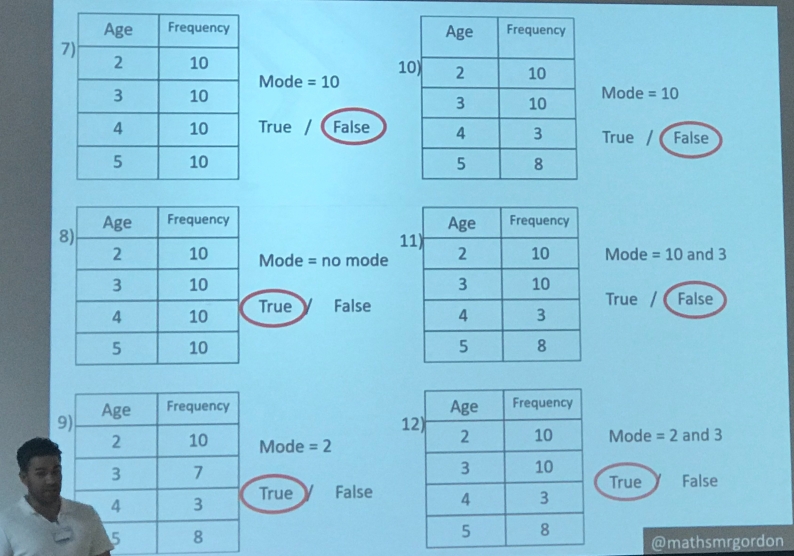 Ben then took the baton to talk about variation by rule, and how he introduces concepts through examples and non-examples, but by varying one thing at a time in his examples. Again, I’ve done some of this, but not to the extent of only changing one thing! And it was hard to come up with the examples and non-examples as my list. Ben’s example of mode from a table was seamless, and his demonstrations of actually how to do it with the class were very useful. A silent introduction whilst students concentrate on the examples, cold calling for reasoning, insisting on correct language, and then class calling!
Ben then took the baton to talk about variation by rule, and how he introduces concepts through examples and non-examples, but by varying one thing at a time in his examples. Again, I’ve done some of this, but not to the extent of only changing one thing! And it was hard to come up with the examples and non-examples as my list. Ben’s example of mode from a table was seamless, and his demonstrations of actually how to do it with the class were very useful. A silent introduction whilst students concentrate on the examples, cold calling for reasoning, insisting on correct language, and then class calling!


 Danielle shared Alibali’s ideas for scaffolding, which reminds me not to always use the same method.
Danielle shared Alibali’s ideas for scaffolding, which reminds me not to always use the same method.
 Initially I wasn’t going to go to Craig’s workshop. Not that I didn’t want to hear what he said, but more that I had already vacuumed up his book in a weekend of frenzied reading, and have listened to many of his podcasts with the experts from which Craig’s reading into the research had originated. How glad I am I changed my mind! Craig is a fantastic speaker and his depth of thought into maths teaching is inspiring. I have no problem in recommending any maths teacher, new or experienced, read Craig’s
Initially I wasn’t going to go to Craig’s workshop. Not that I didn’t want to hear what he said, but more that I had already vacuumed up his book in a weekend of frenzied reading, and have listened to many of his podcasts with the experts from which Craig’s reading into the research had originated. How glad I am I changed my mind! Craig is a fantastic speaker and his depth of thought into maths teaching is inspiring. I have no problem in recommending any maths teacher, new or experienced, read Craig’s  Intelligent practice is something else I am striving towards. At the moment, I attempt it rarely, but it is something that can become a powerful tool in students initial learning and understanding of a concept. Craig’s example with product of prime factors blew my mind! I thought it was genius how the questions develop so students can start to expect a certain answer, and then check it with their learning. And then every now and again a cognitive shock is thrown in when the answer isn’t what they expect and they look to see why, involving the hypercorrection affect (learning is more powerful when you are wrong about something you thought was correct).
Intelligent practice is something else I am striving towards. At the moment, I attempt it rarely, but it is something that can become a powerful tool in students initial learning and understanding of a concept. Craig’s example with product of prime factors blew my mind! I thought it was genius how the questions develop so students can start to expect a certain answer, and then check it with their learning. And then every now and again a cognitive shock is thrown in when the answer isn’t what they expect and they look to see why, involving the hypercorrection affect (learning is more powerful when you are wrong about something you thought was correct). Same structure, different deep problems (SSDD problems) were something else Craig introduced in his book and has since developed. These are problems which look the same, or are in the same context, but have different mathematical requirements for them, as on the example shown (this is one of mine!!). In this case they are different types of percentage questions, but the mathematical concepts in each question does not have to be related. Time for Craig’s second golden nugget – he has set up another website
Same structure, different deep problems (SSDD problems) were something else Craig introduced in his book and has since developed. These are problems which look the same, or are in the same context, but have different mathematical requirements for them, as on the example shown (this is one of mine!!). In this case they are different types of percentage questions, but the mathematical concepts in each question does not have to be related. Time for Craig’s second golden nugget – he has set up another website 
 Then Matt introduced us to his favourite spreadsheet. Just a spreadsheet with cells coloured in red, green or blue, but when you zoom out it’s a picture of Matt! Here’s mine, created from Matt’s
Then Matt introduced us to his favourite spreadsheet. Just a spreadsheet with cells coloured in red, green or blue, but when you zoom out it’s a picture of Matt! Here’s mine, created from Matt’s 
 She gave some excellent phrases to use to support confidence and resilience, as well as ideas for resources that get pupils practising resilience in low entry challenges which can then be used as a starting point to praise the process of resilience. I would highly recommend Sarah’s workshop if she were to do another one.
She gave some excellent phrases to use to support confidence and resilience, as well as ideas for resources that get pupils practising resilience in low entry challenges which can then be used as a starting point to praise the process of resilience. I would highly recommend Sarah’s workshop if she were to do another one.
 From “tricks” for squaring n+0.5 two digit numbers, based on expanding brackets like earlier, to factor skyscrapers, HCF/LCM pyramids, the Ulan Sprial, Goldbach’s conjecture, happy numbers, Kaprekar’s routine, Sierpinksi triangle and Chaos Game to name a few, Johnny provided us with many ideas, with quite a few being being enable from his excellent
From “tricks” for squaring n+0.5 two digit numbers, based on expanding brackets like earlier, to factor skyscrapers, HCF/LCM pyramids, the Ulan Sprial, Goldbach’s conjecture, happy numbers, Kaprekar’s routine, Sierpinksi triangle and Chaos Game to name a few, Johnny provided us with many ideas, with quite a few being being enable from his excellent  Amir took his big 3 – Bloom’s Mastery, Englemann’s Direct Instruction and Cognitive Load Theory and looked at the common themes. He then boiled it down to Question, Model, Check, Praise and Retrieve. It is, of course, a bit more detailed than that! You can find Amir’s slides and handout
Amir took his big 3 – Bloom’s Mastery, Englemann’s Direct Instruction and Cognitive Load Theory and looked at the common themes. He then boiled it down to Question, Model, Check, Praise and Retrieve. It is, of course, a bit more detailed than that! You can find Amir’s slides and handout 