Teaching new spec Alevel Statistics for the first time this year (previously taught S1), so the first time I’ve taught Hypothesis Testing. Having heard one of my Y13 Pure students moan about Hypothesis Testing, I definitely thought I need to be over prepared. At mathsconf, Catriona Agg @Cshearer41 ran a session on Hypothesis Testing for correlation and how she introduced it to her students, so I thought I’d try a similar approach, shamelessly magpieing her brilliant ideas for picturing the situation and probabilities. Using Joe Berwick’s @BerwickMaths notes for statistics (https://berwickmaths.com/2020/05/23/notes-for-year-12-statistics/) to help me ensure I’d got the correct language when talking through the introduction, I put together an ‘almost’ picture story on Ducks and Green (Seier, E. and Robe, C. , (2002), Ducks and Green – An Introduction to the Ideas of Hypothesis Testing. Teaching Statistics Vol 24 Num 3 Pages 82-86 https://onlinelibrary.wiley.com/doi/abs/10.1111/1467-9639.00094).
Hypothesis Testing
L3 Mathematical Studies AQA
1 Year or 2 Years?
On Thursday I hosted a Virtual Community for AQA on Developing the Teaching of L3 Mathematical Studies, concentrating on the 2A option. (Unfortunately 15 minutes in, the tech company hosting the platform had a fire alarm and we were stuck on a chat screen, so 45 minutes were spent type chatting to the delegates, having a general chat about the course – the VC will be rescheduled, hopefully for early December. Really looking forward to connecting to other teachers again).
However, we had managed to get to the part where we discussed advantages and disadvantages of the 1 year or 2 year course. We currently run it as 2 years, but I’m looking to change to a one year course with more lessons per week, as we’ve finished all the teaching and it’s a long time to keep enthusiasm for revision from November until May! The contributions from everyone at the VC were very valuable, and having seen other teachers query this, would like to share here. I’ve anonymised the comments, but haven’t edited any of them. From the poll, most teachers in the VC taught over 1 year, hence the imbalance of comments!
Question: What have you found the advantages of 1 year course?
I don’t know. I only joined the school in September and there was no other option.
Level 3 results available when doing UCAS,
Students can focus on other A levels in year 13
Students who study psychology but gained a 4 in maths. Pupils are more likely to engage with a 1 year course.
Only funded for 1 year
Doesn’t clash with other A’Level exams
Great to have the extra qualification
We have a mixture of Y12 and Y13 students, including those who did not do well enough with A level in Y12.
The real life applications have been invaluable to students
Students studying psychology have a pre requisite of Core Maths if they do not achieve a grade 6 or above at GCSE so helpful for that
Financial maths is invaluable preparation for uni
I’m actually delivering as CPD to other members of staff so the advantage for doing it over 1 year is that they’re able to get it ‘under the belt’ quicker
Can be useful if students are dropping from 3 A’Levels to 2 or are resitting a year but keeping one of their original ones to fill in time on timetable
Doesn’t interfere with the pressure on Students in Year 13. Students find the financial maths both interesting and very helpful.
Question: What have you found the disadvantages of 1 year course?
The exam is set too early (mid May) so less time to revise
Lots of content to get through
Fitting everything in can be a challenge
Time
Time pressure
Getting everything done in time, not alot of time to review learning
Not enough time
Why did they move the exams back to May? Last summer they were in June.
Agreed. Time is a bit tight, especially as I’m in a UTC where we lose lessons here and there for things like careers related days.
Exams have usually been late May, they were only pushed back because of lost learning time due to covid, This mirrors the previous Use of Maths AS Level which it replaced.
Question: What have you found the advantages of 2 year course?
More time in teaching
Extra exam paper practice
I teach Deaf children and they need a lot of help understanding the vocabulary. 2 years allow me to take time to cover the langauge as well as the maths.
Question: What have you found the disadvantages of 2 year course?
Very thin content wise
Difficult to plan
Not knowing how long it takes to teach each part of the content
Supporting Student’s Revision
I ‘attended’ #TMMathsIcons on Saturday (a superb event), and contributed a short presentation on support student’s revision. Attached are my slides and the margin prompts mentioned.
The presentation was about what strategies we have used to support student’s revision, such as explaining about the testing effect from the Roediger and Karpicke (2006a) study, a very non-expert overview of working memory, long term memory and retrieval and quotes (which someone else had previously shared, but awfully, I can’t remember who) about retrieval. We then shared a range of strategies with the students that they can use, strategies that we also use in the classroom, all the time reminding students to keep testing themselves.
The second part of the presentation is about the area of revision that I think I’ve neglected – strategies for selection of methods. To support students in this, we modelled close reading of the question, something I’d been introduced to on a course about the reading challenges of GCSEs. We also used margin prompts, as described by Jacob Wilson, in his Learning to Learn article in the May 2018 Impact, which we break down the phrases “what do you know?” and “what can you do?”, or as Andy Lyons @MrLyonsMaths describes it, “state the obvious, apply the obvious”. I briefly mention in Alevel we look for the trigger words which should trigger knowledge and connections.
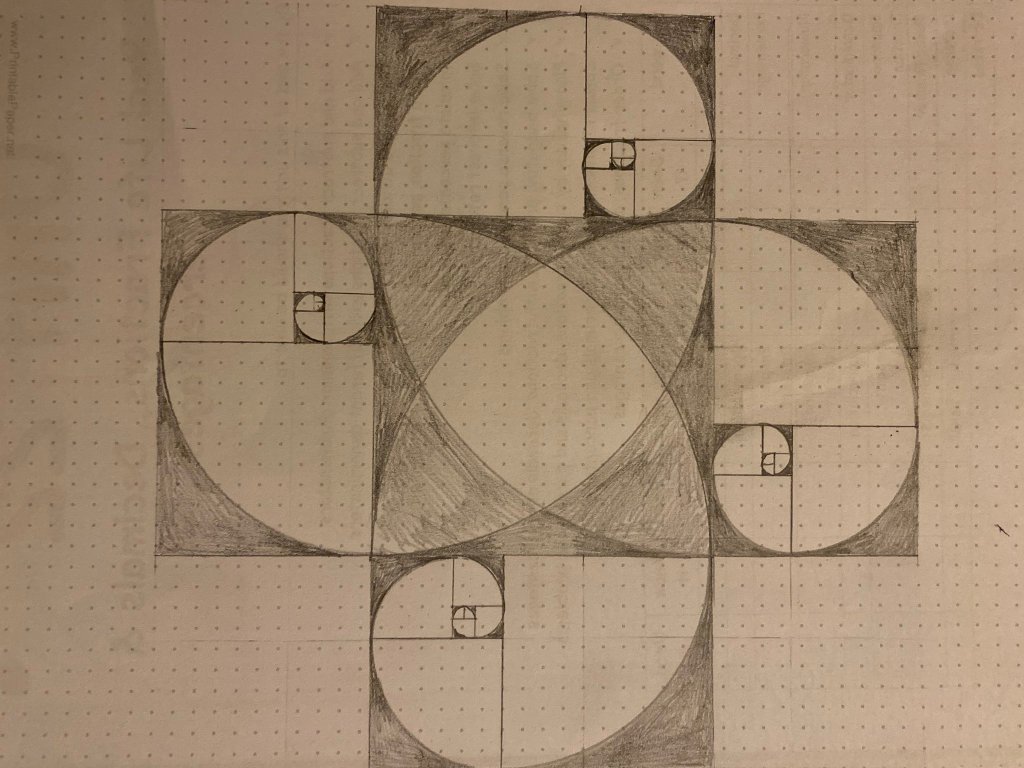
Fibonacci Spiral
To finish our learning about sequences, I introduced my students to the Fibonacci sequence and we had a go at drawing Fibonacci Spirals. The attached ppt includes a link to Vi Hart’s video, a small activity, some art work, and instructions to draw the spiral (although I didn’t actually use the instructions, instead just used the visualiser and worked through with the students).
A Spotlight on Multiplicative Reasoning Part 1
I really enjoyed putting together the workshop for #mathsconf24. These are my slides attached, with what the pen should have looked like when I was attempting to write as I presented. A learning curve for me actually presenting, but I’m determined to get more fluent!
I have been thinking more about the a:b=c:d and a/b=c/d combination as I’ve been planning a similar shapes lesson, but that will be have to be in another blogpost as I am way behind on my planning for Monday!
A Journey into Manipulatives Part 1
For the first time that I can remember, I am in an appraisal process that is aimed at both my development as a teacher and as part of a department. Three specific appraisal targets which I’m really excited to get my teeth into. The plan is to blog about all of these, but one target at a time…
So firstly, my second target is to develop the use of manipulatives in my teaching and to share these strategies with the department. There is a particular focus with my lower prior attaining year 8 group, but not restricted to just this group.
Prior to this year, I’ve started introducing myself to the use of manipulatives with the following:
- Attending a workshop from Johnny Hall @studymaths on the use of double sided counters, including his amazing mathsbot.com website

- Attending a workshop from Bernie Westacott @berniewestacott on the use of double sided counters
- Attending a workshop from Peter Mattock @MrMattock about division, and the use of cuisinere rods
- Dipping into Pete’s book Visible Maths (the negative numbers part so far)

- Attending a workshop on manipulatives and their representations exploring algebra tiles
- Reading Mark McCourt’s @emathsuk book Teaching for Mastery – a huge influence on how I approached and presented
- Attending a workshop from Dr Liz Henning on the use of manipulatives to deepen conceptual understanding (see notes here)
Double Sided Counters
 From these, I have made use of double sided counters when teaching negative numbers. To begin with, I printed out some squares, with a yellow 1 on one side and and red -1 on the other side. A bit fiddly, but did the job as I introduced negative pairs and adding and subtracting with negative numbers. I’ve since upgraded to actual double sided counters (Amazon – 2 packs of 120, so 16 sets of 15 for classroom use).
From these, I have made use of double sided counters when teaching negative numbers. To begin with, I printed out some squares, with a yellow 1 on one side and and red -1 on the other side. A bit fiddly, but did the job as I introduced negative pairs and adding and subtracting with negative numbers. I’ve since upgraded to actual double sided counters (Amazon – 2 packs of 120, so 16 sets of 15 for classroom use).
So to the actual lessons and use of the double sided counters. The learning plan goes like this:
- Use of number line with negatives as starting points or ending points
- Context questions
- Introduce double sided counters
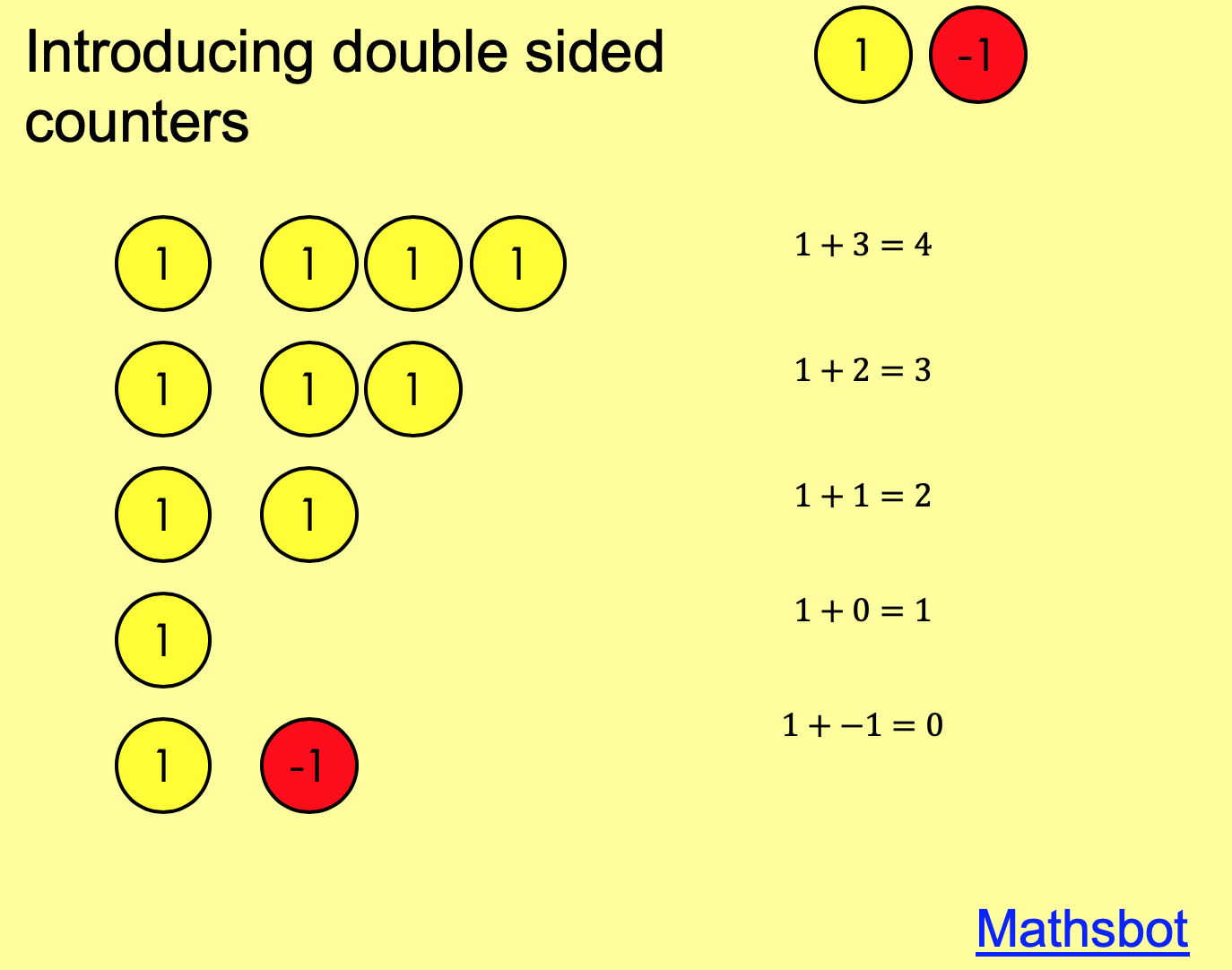
- Zero pair

- Playing with counters
- Adding a negative and seeing result

- Quick questions
- Subtracting a negative and seeing result

- Quick questions
- Mixture of adding and subtracting negative numbers (for some groups I used these questions from variationtheory.com
The powerpoint I made is here: Add and subtract negative numbers. You’ll have noticed the mathsbot.com links – there was lots of talk and playing, with demonstrations using Johnny’s site.
I am still looking to improve and refine, but so far the students appeared to make sense of what was happening. Ideally, I would have liked more time, as always! My year 8 group used the counters to help with the questions, whilst there was a mixture from my year 7 groups. The higher attaining students, who had learned shortcut rules previously, wanted to just use “the rules”. For other students, some fell back on these rules, whilst others were writing out the R and Y to help them.
Mathsconf21
Hopefully this will be a short but informative post! MathsConf21 – my aim was to present but with moving to a new school and going full time I chickened out. But I did get to go to 5 very informative workshops which I can share all about.
Thanks, as always, go to Mark McCourt and his team at La Salle for allowing this affordable and relevant CPD to happen, and to all the amazing teachers who give up their Saturdays to help each other. This is the true meaning of a community. And where La Salle never fail to deliver, this time they outdid even themselves. A big announcement was on the cards, and oh wasn’t it big! Here’s the link: autograph

I am quite excited about learning how to use Autograph properly and sharing especially with my Year 12 students.
There were 5 workshops throughout the day I attended. Rather than write about them, this time I’m going to upload my sketch notes, inspired by the amazing @olicav and @MrsHawthorne maths. These are available as a pdf download here.






I enjoyed being able to bring another puzzle to the tweet up at lunchtime. This conference it was @mathequalslove link to the Fisher maths puzzle Crazy 8s (here) which both exasperated and delighted some willing folks! We will be starting a puzzle club at our school soon and I’m sure the students will get loads of fun, and build lots of resilience, from some of Sarah’s puzzles she shares.
And finally mathsconf wouldn’t be the same without the opportunity to meet up with some lovely Twitter friends the evening before and during the day, and meeting new people as well. As always, a brilliant day – hopefully see you at the next one!
ResearchEd Rugby 2019
 Another Saturday in June and another education conference, and another gorgeous setting, this time in Rugby. The stairs are important – they’re the two spiral flights we went up and down to get to the maths room. Most times when I go to a conference, my exercise is considerably lacking on that day, but ResearchEd Rugby even managed to account for step rate too! There was a good maths line up, which is where I spent most of the day, but I did venture out to a couple of other sessions, so I’ll start with the one I was most excited to go to, and come onto the maths afterwards. (As always, apologies if I’ve misinterpreted anything, or just got it wrong).
Another Saturday in June and another education conference, and another gorgeous setting, this time in Rugby. The stairs are important – they’re the two spiral flights we went up and down to get to the maths room. Most times when I go to a conference, my exercise is considerably lacking on that day, but ResearchEd Rugby even managed to account for step rate too! There was a good maths line up, which is where I spent most of the day, but I did venture out to a couple of other sessions, so I’ll start with the one I was most excited to go to, and come onto the maths afterwards. (As always, apologies if I’ve misinterpreted anything, or just got it wrong).
Oliver Caviglioli
I first heard of dual coding from Peps McCrea, @PepsMccrea, a couple of years ago at the Maths and Science ResearchEd in Oxford. My takeaway then was within powerpoint presentations, and that the brain couldn’t process written text and speech at the same time, so it is better to have a visual on the presentation to go with the speech. This made complete sense, and since then, I’m much more aware in CPD sessions when there’s a large amount of text on the presentation, that I cannot read it whilst trying to listen properly to what is being said.
Last year I prepared some revision powerpoints for our year 10 form tutors, and dual coding came into play in two forms. Firstly, as a revision technique from the LearningScientists.org, as one of the six strategies for effective learning, but secondly in the design of the powerpoint. Similar, when I prepared CPD at the start of the school year about the challenges faced with reading and the new GCSEs, I was very conscience of dual coding, and tried to make the presentation as visual based as possible.
But now was the chance to hear from the expert, and as I tweeted, @olicav did not disappoint. Oliver’s session was very practical based, in that he presented two problems and a solution, with audience participation! I therefore didn’t write much in notes, but then Oliver has a very comprehensive website, olicav.com, where all his diagrams he presented are available (the quote below was also downloaded from there). Spoiler alert though, the summing up for me was:

- Speech and text is linear
- Schema isn’t linear – we think in diagrams
- Text by itself has a computational inefficiency
- Visual and text are separate but associated, and using both together gives double the chance to process and remember (John Sweller’s dual mode presentation)
The example that Oliver used for the computational inefficiency of text greatly resonates with me for some of those longer maths questions where there is so much information to pick apart. I’m already very much a fan of a diagram or picture, but maybe I need to consider raising the importance of this earlier on for students, even spend time just trying to turn questions into diagrams as an exercise in itself.
The final part was our participation in a recount and redraw exercise. Oliver (as the teacher) modelled, via a mind map diagram, and explained, via speech, a history of Corsica. We, as the student, copied the diagram as Oliver was explaining it. The student then recounts the diagram to a peer, tracing the elements and elaborating on what they have written as they go. Finally, the student redraws the diagram from memory, noting that the retrieval practice would be even more effective if the student did this again a day later and a month later.
Mark Lehain
First of all, Mark is an absolute gentleman, and was very kind in giving his time after the presentation! Mark, @lehain, was talking about behaviour, and from the point of view of a Head Teacher, how teachers can help SLT. Some highlights that I took from Mark were:
- Parents and teachers for excellence – a group that believes that every school child should have an excellent education, and that the key characteristics of those schools that deliver this are excellent behaviour, a challenging curriculum, rigorous testing and enriching extra-curricular activities.
- Recommending Tom Bennet’s Creating a Culture, and in particular the 8 principles of designing a culture.
- Differences of opinion between SLT and teachers may be there because of different experiences, different values or different analyses of situations.
- If you asked “What is the point of education”, there would be different responses. So if we can’t agree on the why, then we’re probably not going to agree on the how. However, we need to disagree well (we’re all a team, working together for the students, and we all have feelings).
The point about disagreeing well particularly resonated for me in the way some educationalists respond on Twitter. I think I would respond so much more if we could all disagree well (or maybe I just need to be 10% braver)!
Don Steward
Now the maths bit! I love Don Steward’s resources. They are so thoughtful of the maths, the connections and the applications, so it’s a real pleasure to explore some maths with Don. Don took one of the Edexcel ratio questions from this year as a starting point to explore ratio. The question involved a ratio of counters, which when other counters (of both types) were added, the ratio changed. This was a lovely practical session, where it’s just great to have some time to explore some maths. We looked at the different methods to solve this question, and the links between. A snapshot of the session includes:
- Establishing what a ratio is (and it being ok to ask students the obvious questions)
- Using scaling to answer the question (testing it out with values and seeing what works)
- Introducing a multiplier to a ratio when introducing ratio (so 4:3 would be 4k:3k) and therefore allowing an algebraic solution
- Graphing ratios and linking to vectors to move from one graph to another – this developed could be developed into a vector method to solve the problem, and also links to a simultaneous equation method
- Developing the question to find the possible number of counters added to change the ratio, which led to sequences and nth term
- The work of Van Hiele, the avoidance of fractions and the proportion matrix
- The ICAAMS project, where year 8 students were given 2 questions, which both use the same method, but had a large variance in success rate.

I’ve been teaching proportion with year 8s this week, and a started using Don’s resource on proportion boxes, as I wanted students to be able to understand that proportion was a multiplicative relationship, and that relationship can go either way. So I’m going to give these two questions to my year 8s and hope that the work we’ve done will make some difference to their success rate with the first question compared to the second.
Jo Morgan
It is always a pleasure to listen to Jo, @mathsjem, on whatever topic she is talking about, because you can guarantee that she knows that topic in depth before she presents it. Jo also gives some great nuggets of practice or exploration and takeaways, which again her multiplication session delivered brilliantly. Highlights:
- A method for any single digit multiplication greater than 5×5 (and a chance to prove why it works).
- Jo’s thoughts on why timetables fluency is important (and I completely agree that although we can and do teach students how to work out timetables without having to know them off by heart, this is no good when the reverse is required, eg for simplifying fractions or factorising).
- A review of different multiplication methods from Smile’s “Multiplication makes sense” and an explanation as to why the Russian Peasant Method works.
- A presentation on the column method, and an argument against each of the reasons given for it to be a “formal written method”. This was not having a go at the column method, just the reasoning given at the time.
Thanks Jo!
Tom Francombe
I hadn’t heard Tom speak before, but I am more than familiar with his book, Practising Mathematics, that I have open on my desk at home pretty much constantly! As Naveen, being a victim of the train problems, was unable to make her session later on, Tom stepped in and did two sessions. Part one was more about the theory, whereas part two was a chance to try some practice.

Who knew there were so many types of practice? Although Tom started with deliberate practice, he explained how really this is unfeasible in the classroom, as it involves immediate feedback on mistakes and altering the practice in light of this. So his talk was more about purposeful practice, an in-between of naive practice and deliberate practice.
Tom talked about fade feedback, which I hadn’t heard of as a term before, but in practice are techniques that I do use in the classroom. As the term suggests, fade feedback reduces the level of feedback that a student receives when solving problems, but based on how the problem is prevented. So the structure could look like the following:
- Initially give the answers, in “show that…” style questions
- Then have answers available to match
- Structure questions so the answers have some sort of commonality (Don’s resources have some good examples of this)
- No answers available.
Tom also spoke about organising practice, comparing blocked practice and interleaving, and within the interleaving, either mixing different questions (such as multiplying fractions and finding areas of kites), or mixing topics within the question (finding areas of kites with lengths as fractions). This is an important area of contemplation for me at the moment. I use spaced practice in my BBQ starters for KS4, and my homework and quizzes for KS3, but I don’t interleave in “main” classwork, unless it’s part of revision. Yet, as Tom pointed out, in maths we have to choose our strategies before we use them, which is not addressed in blocked practice. This isn’t to say blocked practice doesn’t have a place, and Tom emphasised that with first learning, blocked practice would be more suitable. This is definitely an area I need to think more on!
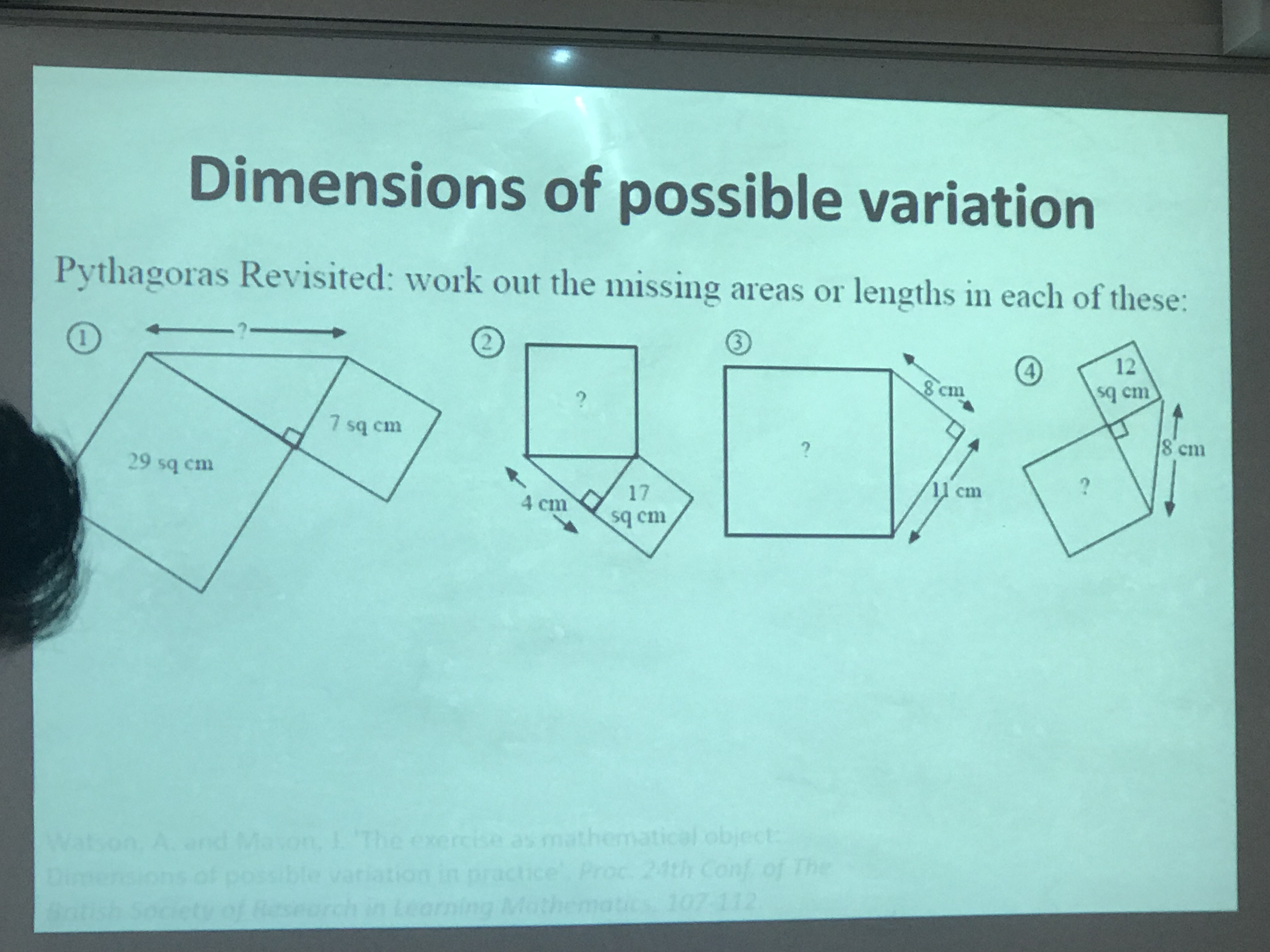 When presenting some of the possible ideas of practice tasks, Tom’s purpose was to find tasks that can develop fluency, but also allow for mathematical reasoning. He indicated that the research said that these tasks were as effective as straight forward exercise tasks, but they can be more motivating and enriching.
When presenting some of the possible ideas of practice tasks, Tom’s purpose was to find tasks that can develop fluency, but also allow for mathematical reasoning. He indicated that the research said that these tasks were as effective as straight forward exercise tasks, but they can be more motivating and enriching.  We had a go at a few of these; this Pythagoras task adds another dimension to your normal “square, square, add or subtract, square root” type questions, and the multiplication task (which I’ve used before) gave us chance to explore some reasoning.
We had a go at a few of these; this Pythagoras task adds another dimension to your normal “square, square, add or subtract, square root” type questions, and the multiplication task (which I’ve used before) gave us chance to explore some reasoning.
Pete Mattock
The great thing about attending one of Pete’s session (as well as his presentation) is that we get to play! This time, Pete, @MrMattock, brought his algebra tiles along. I’m very much a newbie with manipulative, only really having access to multilink cubes. I did make my own +1/-1 counters this year for teaching negative numbers, which I loved using!
However, Pete’s session wasn’t actually about manipulative, they were just a bonus. Pete was talking about the concepts of Teaching for Mastery (as described by the NCETM), Rosenshine’s Principles of Instruction and Sweller’s work on Cognitive Load Theory. Pete suggested that rather than look at them as three separate entities, we can find the overlaps between them, as then we’d be looking at the overlaps between high performing jurisdictions (Teaching for Mastery), high performing teachers (Rosenshine’s Principles of Instruction) and how the memory works (Cognitive Science).
I made the mistake here of listening and doing so much, that I didn’t write any notes! Pete gave some lovely examples of how these three concepts (is that the right word to describe them?) are used together, but I don’t trust myself to recall these accurately enough to describe (sorry Pete!).
Curriculum Ed 2019
I toyed with writing a post about Curriculum Ed, mainly because I didn’t want to misinterpret any of the vast information that was presented by speakers far more knowledgeable than myself. But then if I have misinterpreted, it could always be a starter for discussion, and I’ve been really keen to think through what I’ve heard, and the best way to do that is through writing about it.
The Ofsted bit
Although Sean Hartford (@HarfordSean) didn’t start the conference, it is his talk that introduces the focus on curriculum. There’s already been quite a bit of comment over what Sean said, the two “controversial” points being that both academisation and Ofsted’s focus on data have led to a narrowing of the curriculum in English schools, and that Sean can’t believe that over 90% of schools have good behaviour, despite Ofsted figures showing this. I, for one, am pretty pleased that Ofsted are reviewing their practices and looking to improve, rather than thinking it’s already good enough. Isn’t that what we all do? The behaviour issue was with respect to schools being able to support students for one, or two, days to be on their best behaviour! It will be interesting to see Ofsted’s approach develop, as the initial idea of talking to those who get the brunt of poor behaviour does feel like it may have a few road bumps in the way. With regards to the personal development part, Sean did say that schools can’t solve society’s problems by themselves, but they can implement quality programmes that will support in this quest.
So by reviewing the framework, Ofsted have developed the Quality of Teaching judgement to include a focus on curriculum, and particularly a curriculum which has a narrative, otherwise it only serves the top few percentage of students who remember everything. The curriculum shows the intent, but Ofsted will also be looking at how this is enacted in the classroom. Ofsted will go from top level overview discussions with subject leaders, and then making a “deep dive” into classroom practice for current aspects of the curriculum, looking at books whilst in discussion with teachers and students. For me, the opportunity to explain my pedagogical reasoning for what and how I’m teaching is really positive, rather than a judgement with no discussion. Sean did talk about group work verses Direct Instruction, emphasising that research has shown both methods to be effective, if either are implemented in a way that makes them effective.
Along with the three keynote speakers, delegates all had the daunting job of selecting which 3 speakers’ sessions they would attend out of a cast of 20. Not an easy choice with the calibre of speakers there. For the sessions I attended, there were two main themes. One being curriculum as a narrative and the other along the lines of what do we teach and powerful knowledge.
Curriculum as a narrative
Clare Sealy (@ClareSealy) stepped in to open the conference as Christine Counsell (@Counsell_C) was not at all well at the start of the day (and very graciously, Christine hung around and spoke for the final keynote, and on her birthday no less!). Before developing the metaphor of the curriculum being like a box set, Clare took a few minutes to revisit building schema, and the differences between assimilating schema (nicely slotting in new knowledge to what we already know) and accommodating schema (where we have to rearrange what we know to take into account the new knowledge), as described by Piaget. Although both are a part of progress, it is the accommodation that plays the more significant part.
The box set metaphor comes in the difference between a series, such as The Simpsons, and a serial, such as Game of Thrones. Whereas the series are a group of stand alone stories, a serial will build over time, with both character development, sub plots that link into the main plot and conflicts. I’d never heard of the phrase “Chekhov’s gun” before, but liked the idea that if something is going to be a part of the narrative, there needs to be a reason for it. Clare went on to extend the metaphor to show how in her setting, primary, they are creating a whole Chekhov’s armoury for KS3.
Christine also spoke on a similar context for secondary English and Humanities. Using the example of teaching Animal Farm at KS4, Christine suggested how much richer the learning could be had the students been exposed to the Russian Revolution in KS3 and taken that knowledge into their Animal Farm lessons for the English teacher to draw upon and extend in terms of the literature. This is then a narrative that goes across subjects in the curriculum.
Clare explored how a serial of lessons would look, beginning with quite shallow learning where what could seem to be unconnected bits of knowledge are introduced. In subsequent lessons though, the students are being directed to the knowledge required to make connections. These begin with the “Previously…”, recapping those bits of knowledge which need noticing as students start to accommodate new knowledge in their schemes. This all leads to the deep learning, “to understand the relationship of the parts” (Willingham).
Knowledge, Powerful Knowledge and Knowledge about Knowledge
To quote Christine from the end of the conference “teachers must have a relationship with the knowledge they teach”. Earlier, I attended an encapsulating session from Di Swift “Enabling Teachers to Build Knowledge about Knowledge”, which echoed Christine’s sentiments.
I discovered here that there were far more types of knowledge than I realised, and came across the term “Social Realist” for the first time, which I’ve been able to delve a little more into since Saturday. Di differentiated between craft knowledge, the know how, and the need to understand the why. This was aimed particularly at teachers being able to explain their pedagogical reasoning for what and how they are teaching, and I would imagine links in to what Sean was saying about the deep dive when making judgements about the curriculum and how it is enacted in the classroom. Di also pointed out how activities should serve the knowledge being taught. This is something I’ve been passionate about when planning and working with ITTs; that we begin with knowing what we want students to learn, and the resources we use have to fit into this.
Ruth Walker’s (@RosalindPhys) session was entitled “Powerful Knowledge”, and I could tell that she was very passionate about the works of Michael Young and, for her, the importance of implementing this into schools in the most effective way possible. Di had already introduced Michael Youngs opinion on Powerful Knowledge to me in her session, and how this changed over time, from an elitist version of just forcing what powerful people thought was knowledgable onto others, to a knowledge that is empowering and allows others into making informed choices about that knowledge.
Ruth used the definition of powerful knowledge as a combination of both substantive knowledge and disciplinary knowledge. Although Ruth gave definitions in her presentation, I needed more clarification, and found Christine Counsell’s description in her article for Impact (Taking Curriculum Seriously, Sept 2018) to help: “Substantive knowledge is the content that teachers teach as established fact….Disciplinary knowledge, by contrast, is a curricular term for what pupils learn about how that knowledge was established, its degree of certainty and how it continues to be revised by scholars, artists or professional practice.”
Martin Robinson (@Trivium21c) also spoke about powerful knowledge in his presentation “Cultural Mobility: An Argument Against Instrumentalism”. His description included 4 parts: knowledge that moves beyond the particulars of experience; knowledge that makes sense of and improves the world; knowledge that is cognitively superior to that needed for daily life; and a knowledge that is distinct from common sense knowledge.
Di continued with her presentation to introduce Legitimation Code Theory, and in particular Semantics. 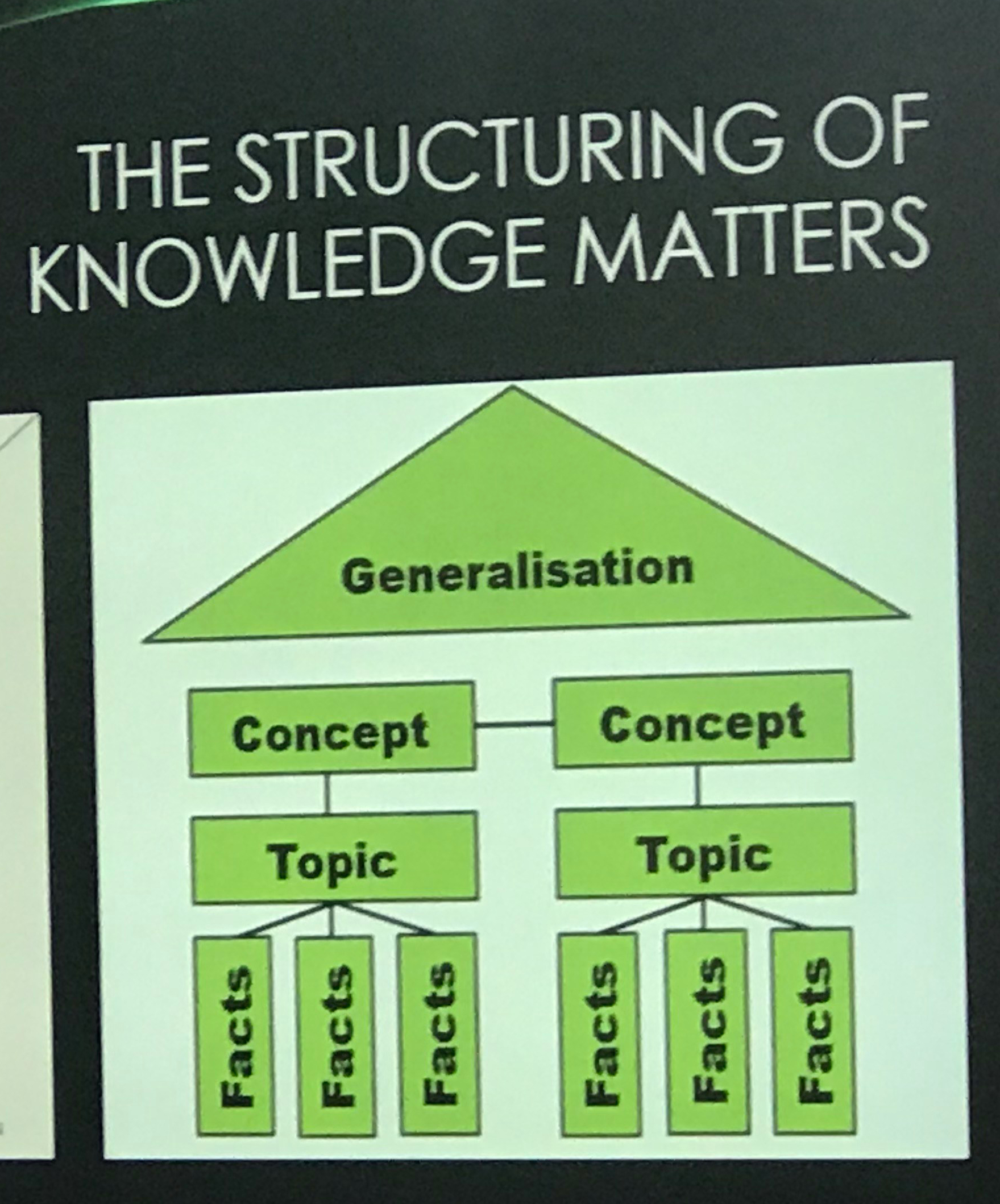 This is something new to me, but I the main idea I took away was that knowledge was built through the relationship of contextual knowledge and “the big ideas”, and travelling between these two parts will improve understanding. I imagine this to be similar to Piaget’s accommodating schema. Di believes that the best education system is one where the curriculum is coherent, and the concepts are organised. Therefore when planning, it should be the concepts that are planned for first, then the context (topic) and finally the cotnent (facts).
This is something new to me, but I the main idea I took away was that knowledge was built through the relationship of contextual knowledge and “the big ideas”, and travelling between these two parts will improve understanding. I imagine this to be similar to Piaget’s accommodating schema. Di believes that the best education system is one where the curriculum is coherent, and the concepts are organised. Therefore when planning, it should be the concepts that are planned for first, then the context (topic) and finally the cotnent (facts).
Ruth continued passionately talking about powerful knowledge, with her 10 points about knowledge. Point 8 stood out for me, “It is fair and just that all children should have access to this knowledge”, reinforcing what Ruth mentioned earlier in her presentation, that “background and social class shouldn’t determine what is being taught”. In order to implement this powerful knowledge in a curriculum in schools, Ruth identified 3 key areas that needed to be addressed in order for it to be implemented successfully:
- Get behaviour right – teachers need to be able to teach with a crystal clear policy;
- Share the vision and intellectualise the staff – one way this can be done is through reading, whether book, blogs, twitter, journals etc.; and
- Treat it as a grand project and project manage it.
Ruth will be presenting again at ResearchEd Rugby, 15th June 2019.
For Martin, I understood that he was expressing that powerful knowledge, along with some other aspects of culture capital, is not enough to enable the main function of the curriculum, which is to provide meaning. Martin began with meritocracy – that those with the IQ and effort will result in merit – and claimed if the belief success is down to your IQ and merit, then if you are not successful then it is also down to you. Next was Habitus and cultural capital – if you take on the right cultural habits then you can move up the success scale – so that IQ and effort now results in social status, leading to social mobility. But he says that the only time in history this has changed is following the second World War. Martin also mentioned cultural literacy, and how culture had acquired a snob value – something that’s only needed to get on in the world.
Martin closed by asking the question, “how do we give students the space for freedom to think for themselves?”, and the desire for the pursuit of knowledge. He described his T shaped curriculum, which gives breadth for a foundation of knowledge, before going into depth, and leads students to make their own decisions. So instead of teaching, as Arnold describes, “the best which has been thought and said in the world” as an aim, bring students to the point where they can be part of the conversation of what the best might be.
A Conversation with Culture
Christine concluded the day at Curriculum Ed, with her talk about “Curriculum as a Conversation with Culture”. I enjoyed being able to just listen to Christine talk, although it did mean that I don’t trust myself to write about some of her presentation, but I did take away a few notes and interpretations of the latter part of her talk.
Firstly, the more you know, the more you see when introduced to new material. Secondly, difficulty is relative to degrees of familiarity, and familiarity can be crafted. Thirdly, every subject is a pursuit of Truth, and as teachers we should be clear that what I’m teaching is not all there is; it is just a selection.
In conclusion, Christine spoke about 3 common muddles when looking at, or designing the curriculum:
- That curriculum design is treated as an audit – an aggregate of its parts, rather than a narrative. Christine reinforced that the curriculum is a narrative, and that we must know why each part of the curriculum specifies that part of knowledge. This also included the idea of muscle memory – that time spent on the basics releases time, and allows for creativity later.
- Treating all subjects the same.
- The failure to treat the curriculum as a sum of its parts. Christine used the example of teaching Animal Farm as a KS4 novel, and how much richer the teaching could be if students had been prepared in history in KS3 with the teaching of the Russian Revolution.
So an excellent day was had at CurriculumEd. I apologise if I have misinterpreted, or written something wrong! Thanks of course go to all the speakers who gave up their time to present (the only disappointment being that I missed out on some as there was too much excellent choice), and to Steve (@SputnikSteve) and Jo (@joanneowens) and their team for organising an excellent conference.
MathsConf15 Takeaways
With exam marking starting, I’ve only got chance for a quick blog about MathsConf15, mainly giving me a chance to organise my thoughts, but if anyone else can take something away then that is a bonus! No Friday night socialising for me this time, which meant not much chance to catch up with the lovely folks I’ve got to know during mathsconfs. So I’ll dive straight in!
Workshop 1 – Core Skills: Defining the basics
Ben Rapley took us on a a tour of how they have included a focus on improving core skills alongside their scheme of work in his department. Through departmental discussions, they selected 7 key topics that are essential, and regularly used in multistep problems: Fractions, decimals, percentages, ratio, negative numbers, brackets and equations (this was stage 2; stage 1 topics were: addition, subtraction, multiplication, division, number properties, place value and collection like terms).
Already, I’m liking this workshop! I’m currently working on building more number sense into our scheme of learning from year 7, and the stage 1 topics, except for collecting like terms, were pretty much the same as what I had!
Ben’s department created a core skills development ladder for each of the 7 topics. Looking at brackets on our table, you realise how quickly the ladder could be enormous! But as Ben said, these are organic creations which change as you use and need to tweak them.
The next part was about the assessments. For Ben’s department, they do 1 assessment per half term, and everyone on stage 2 (from year 7 to 11) do the same assessment. This is an interesting idea, and the question was asked about motivation for some students who may score poorly on it.
The assessment lasts 1 and a half hours and has 15-20 questions per topic – a question for each sub-part of the ladder. The 2nd half of the lesson is self-assessment, and here Dylan William’s quote about the research comes into play, where students that self-assessed progressed more than those that peer assessed or had their work teach assessed. The next lesson was feedback, often whole class verbal and modelling target questions. Every lesson after that had starters related to the targets.
The assessment set up is a big step away from ‘normal’ termly assessments, being one mark per skill, and total fluency without context or multisteps. The big takeaway for me here though, is the excel spreadsheet used to generate the questions! I need to do a bit of work, but currently I have weekly quizzes for years 7 and 9 (I don’t currently teach 8) and daily starters for year 10, which if I could press F9 and do some of the amazing things the spreadsheet does, then it would be such a time saver!!! I was almost drooling when Ben explained that you choose your click on the questions and they appear in a worksheet, which could also be changed to a project view. Might be watching a few ‘Excel how to’ videos over the holidays.
Ben finished with talking about interleaving the core skills throughout the scheme of work; again something that I am looking at with the number sense work for Year 7, with the example of using fractions when calculating perimeter or area. This is something I also want to think more about within my teaching, so that it’s not just the weekly quizzes or daily starters that cover topics taught, but they’re intertwined throughout future learning.
Workshop 2 – Procedures are not the enemy
I hadn’t realised when I went to Andy Elwell’s workshop that he was the creator of Method Maths. I hadn’t come across it before this year, but have been very impressed with how the year 11 were using it to practise, practise, practise this year!
Andy started with a tour of how multiplication is taught from year 1 to year 6. The stand out point of this was the journey from concrete, with lots of manipulative, to more abstract (ie just written) in Year 6. Andy then demonstrated the number of steps needed to complete a column method multiplication, compared to the lattice method. 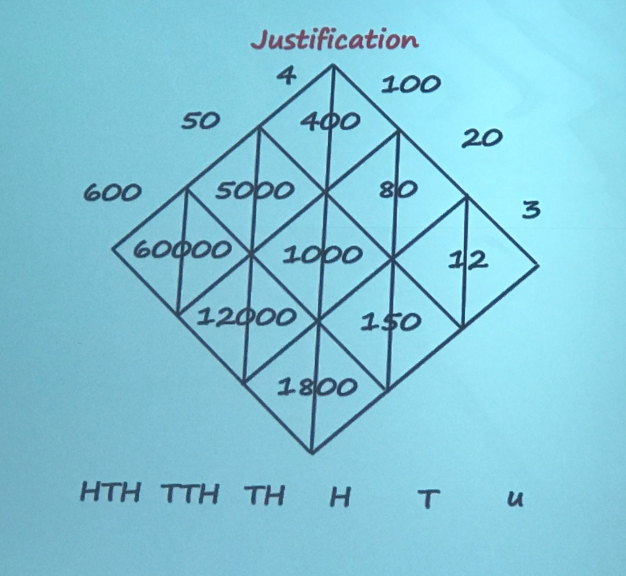
The immediate murmuring was about how the lattice method does not help students understand the place value in multiplication and it was just learning a procedure. However, Andy was ready for this, and showed a neat justification of why the lattice method works, by rotating a multiplication grid. The question to consider is, why don’t we let students use easier methods, as long as we keep it conceptually connected justifiying why they work? So my first takeaway – should we teach our year 7s the lattice method when they arrive, alongside why it works?
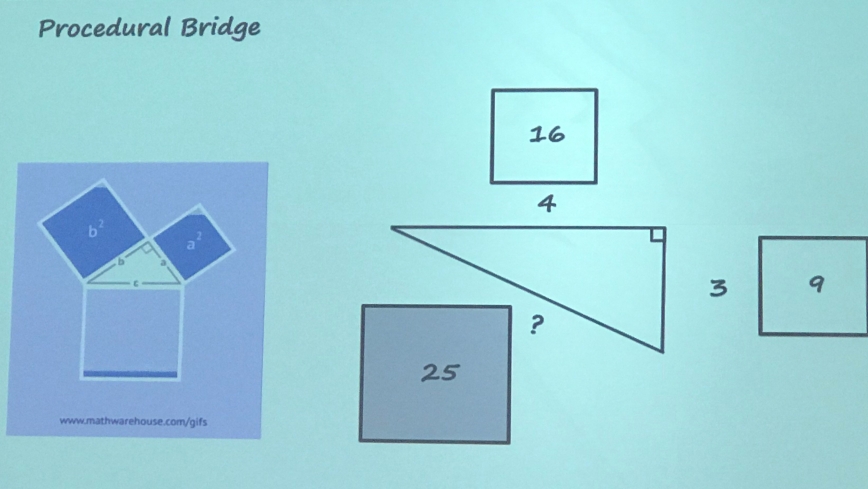 The next idea was a game changer for Andy, and I love it! I wouldn’t even call it a procedure, but more making Pythagoras’ Theorem a bit more concrete, rather than the abstract algebra workings. I (and I’m sure many do) introduce Pythagoras looking at the square of the sides of the right angled triangle. Well why not draw squares next to each side and put the square value in?
The next idea was a game changer for Andy, and I love it! I wouldn’t even call it a procedure, but more making Pythagoras’ Theorem a bit more concrete, rather than the abstract algebra workings. I (and I’m sure many do) introduce Pythagoras looking at the square of the sides of the right angled triangle. Well why not draw squares next to each side and put the square value in?
We were now starting to get, on what Andy believed to be, more controversial ground. The DM method! And I’d agree, if it was introduced as a process with no understanding, it would be controversial. So what is it?!  The DM method is basically a procedure to use for any maths that can be set up in proportional grids From ratios, to map scales, equivalent fractions to even inverse proportion.
The DM method is basically a procedure to use for any maths that can be set up in proportional grids From ratios, to map scales, equivalent fractions to even inverse proportion.
And all it is is “divide, multiply”. But of course there is a justification – dividing establishes scale factor and multiplying applies the scale factor. This is definitely something that I want to explore.
The final idea we unfortunately didn’t get to explore as much as was possible in the workshop, but again is something I’d like to revisit, even if just for my interest. Andy has stopped starting trigonometry with SOHCAHTOA, but introducing trig using the Sine Rule.
Plenary Session – From Fermat to The Simpsons
How amazing to have Simon Singh, mathematician (background is mainly Physics), author, and one of the writers of The Simpsons to deliver a midday plenary session. Simon talked to us about some of his books: The Bible Code (and how for every prediction found in the Bible Code, one is also found in The Moby Dick Code!); Fermat’s Last Theorem; The Simpsons and their Mathematical Secrets (which I’ve read and enjoyed). It was a pleasure just to listen to Simon and his enthusiasm about his work.

Simon also mentioned some of the maths projects that he’s running for schools. For post 16s there is “Who wants to be a mathematician” – more can be found at http://goodthinkingsociety.org; and for KS4 Top-Top Set and Parallel https://parallel.org.uk, which is well worth an investigation.
Workshop 3 – Problem Solving
Claire took us on a tour of problem solving and some of the research around it.  She looked at some of the definitions that have been given about problem solving and shared what what I thought was a great summary: challenging for individual learners; involves a strategy for solving that is not immediate or obvious and involve independent thought and creativity. Problem solving is another of my projects in our department, as we develop our SHAPED problem solving (taking the SHAPED genius of my HOD to implement it effectively to improve problem solving – hopefully more on this to come).
She looked at some of the definitions that have been given about problem solving and shared what what I thought was a great summary: challenging for individual learners; involves a strategy for solving that is not immediate or obvious and involve independent thought and creativity. Problem solving is another of my projects in our department, as we develop our SHAPED problem solving (taking the SHAPED genius of my HOD to implement it effectively to improve problem solving – hopefully more on this to come).
Claire looked at the why of problem solving and what we have to consider when problem solving with out students – some really useful considerations: cognitive load of the students; surface and deep structures (I really like the idea of trying to sort problems into similar groups, where there are multiple groups possible); growth mindset; generic problem solving skills (and whether there are any??!! but also identified the work of Polya’s 4 stages, which is what we’ve also used in our SHAPED problem solving) and topic specific problem solving skills.
Workshop 4 – Variation in mathematics
“Reflect, Expect, Check”
A treat of a workshop to finish, with Craig Barton, Jess Prior and Ben Gordon doing a triple act on how they’ve used variation theory in their teaching. Craig began, introducing 4 ways in which he uses variation theory: by example, by rule, by pattern and by demonstration. Then it was over to Jess to explain how she uses variation by example as an intelligent practice exercise. I love these!! I’ve started using them with some of my classes after reading Craig’s book, but without the full “reflect, expect, check” experience. However, they have already allowed questions and discussions about what is happening. The point is, instead of having unrelated practice questions, change one thing each time, so that the students have the opportunity to think about what’s changed and what effect this will have. At this point, it’s worth pointing out that from Craig’s point of view, this is one tool to use whilst giving student a wide diet of maths. I was so engrossed, I didn’t even get any pics! But Jess has very helpfully written in far more detail on her blog here at minimallydifferent.wordpress.com.
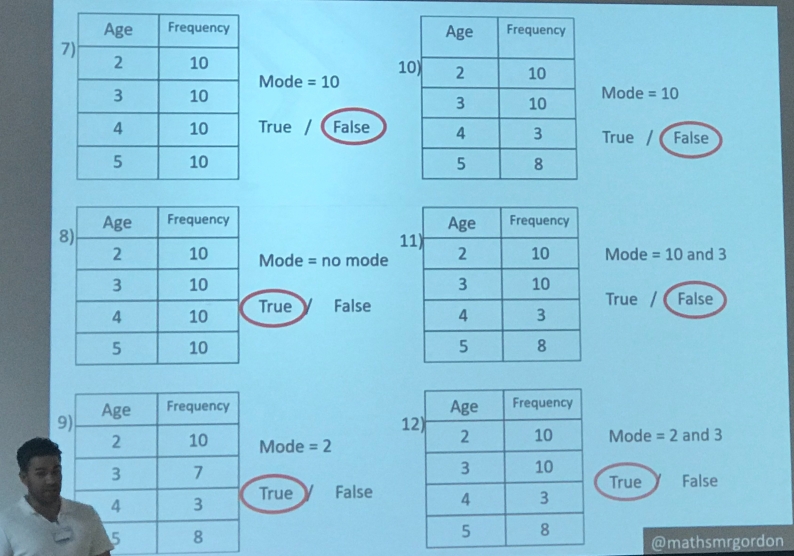 Ben then took the baton to talk about variation by rule, and how he introduces concepts through examples and non-examples, but by varying one thing at a time in his examples. Again, I’ve done some of this, but not to the extent of only changing one thing! And it was hard to come up with the examples and non-examples as my list. Ben’s example of mode from a table was seamless, and his demonstrations of actually how to do it with the class were very useful. A silent introduction whilst students concentrate on the examples, cold calling for reasoning, insisting on correct language, and then class calling!
Ben then took the baton to talk about variation by rule, and how he introduces concepts through examples and non-examples, but by varying one thing at a time in his examples. Again, I’ve done some of this, but not to the extent of only changing one thing! And it was hard to come up with the examples and non-examples as my list. Ben’s example of mode from a table was seamless, and his demonstrations of actually how to do it with the class were very useful. A silent introduction whilst students concentrate on the examples, cold calling for reasoning, insisting on correct language, and then class calling!
Both Jess and Ben came across as if they’d been hosting workshops to a packed lecture theatre alongside “famous” maths teachers for years, and not that it was their mathsconf debut! Craig then finished off with the other two variation methods, firstly making sure that if you are to use a pattern that to make sure it doesn’t become a pattern filling exercise, you leave a “gap of understanding” for students to identify the pattern, see what is happening, and use to predict the results. Finally with regards to variation by demonstration, the key point was to keep the initial diagram for a reference point. I really need to learn how to use geogabra!
Of course, Craig these days does not finish a workshop without an announcement, and true to form, there was an announcement at the end of this one. Craig, Jess and Ben have created a new website called variation theory.com. This will become a collaborative website with all things variation!
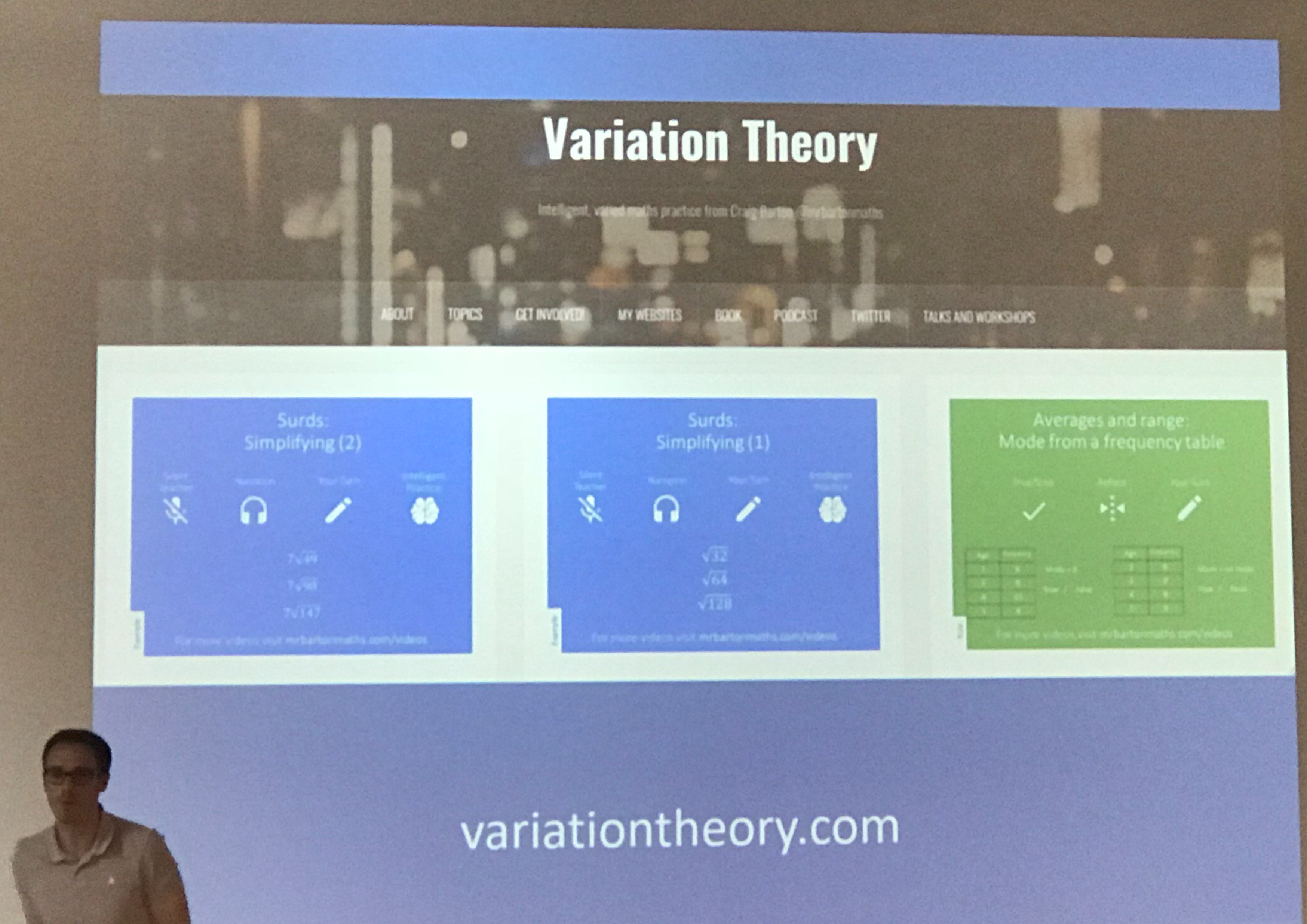
Final thoughts
If you haven’t been yet, you must go to a mathsconf. The CPD for maths teaching is amazing and the willingness to share in second to none. I was very excited to hear that mathsconf17 will be in my home town of Sutton Coldfield! Asking Mark whereabouts, he couldn’t remember but suggested I do a workshop. I had the intention before, but expressed how all that I know is what I’ve read about and heard about from other more expert people than me! Yet the kind Kris Boulton suggested to make that the basis of my workshop, as many other teachers won’t have read these, or heard about them. So, watch this space!

