With exam marking starting, I’ve only got chance for a quick blog about MathsConf15, mainly giving me a chance to organise my thoughts, but if anyone else can take something away then that is a bonus! No Friday night socialising for me this time, which meant not much chance to catch up with the lovely folks I’ve got to know during mathsconfs. So I’ll dive straight in!
Workshop 1 – Core Skills: Defining the basics
Ben Rapley took us on a a tour of how they have included a focus on improving core skills alongside their scheme of work in his department. Through departmental discussions, they selected 7 key topics that are essential, and regularly used in multistep problems: Fractions, decimals, percentages, ratio, negative numbers, brackets and equations (this was stage 2; stage 1 topics were: addition, subtraction, multiplication, division, number properties, place value and collection like terms).
Already, I’m liking this workshop! I’m currently working on building more number sense into our scheme of learning from year 7, and the stage 1 topics, except for collecting like terms, were pretty much the same as what I had!
Ben’s department created a core skills development ladder for each of the 7 topics. Looking at brackets on our table, you realise how quickly the ladder could be enormous! But as Ben said, these are organic creations which change as you use and need to tweak them.
The next part was about the assessments. For Ben’s department, they do 1 assessment per half term, and everyone on stage 2 (from year 7 to 11) do the same assessment. This is an interesting idea, and the question was asked about motivation for some students who may score poorly on it.
The assessment lasts 1 and a half hours and has 15-20 questions per topic – a question for each sub-part of the ladder. The 2nd half of the lesson is self-assessment, and here Dylan William’s quote about the research comes into play, where students that self-assessed progressed more than those that peer assessed or had their work teach assessed. The next lesson was feedback, often whole class verbal and modelling target questions. Every lesson after that had starters related to the targets.
The assessment set up is a big step away from ‘normal’ termly assessments, being one mark per skill, and total fluency without context or multisteps. The big takeaway for me here though, is the excel spreadsheet used to generate the questions! I need to do a bit of work, but currently I have weekly quizzes for years 7 and 9 (I don’t currently teach 8) and daily starters for year 10, which if I could press F9 and do some of the amazing things the spreadsheet does, then it would be such a time saver!!! I was almost drooling when Ben explained that you choose your click on the questions and they appear in a worksheet, which could also be changed to a project view. Might be watching a few ‘Excel how to’ videos over the holidays.
Ben finished with talking about interleaving the core skills throughout the scheme of work; again something that I am looking at with the number sense work for Year 7, with the example of using fractions when calculating perimeter or area. This is something I also want to think more about within my teaching, so that it’s not just the weekly quizzes or daily starters that cover topics taught, but they’re intertwined throughout future learning.
Workshop 2 – Procedures are not the enemy
I hadn’t realised when I went to Andy Elwell’s workshop that he was the creator of Method Maths. I hadn’t come across it before this year, but have been very impressed with how the year 11 were using it to practise, practise, practise this year!
Andy started with a tour of how multiplication is taught from year 1 to year 6. The stand out point of this was the journey from concrete, with lots of manipulative, to more abstract (ie just written) in Year 6. Andy then demonstrated the number of steps needed to complete a column method multiplication, compared to the lattice method.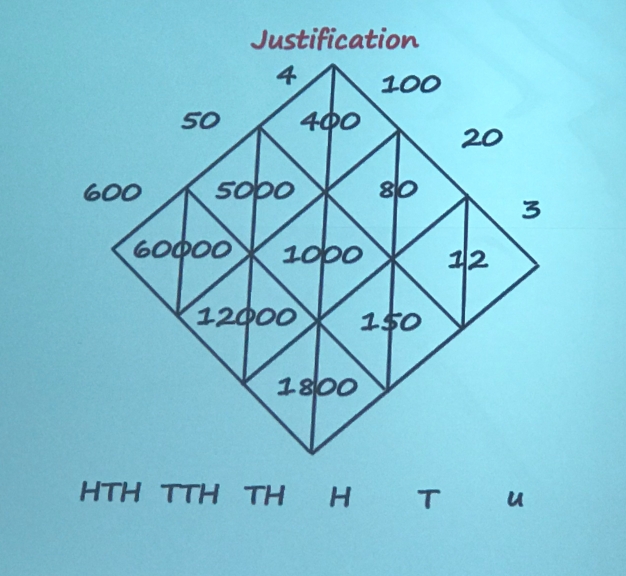 
The immediate murmuring was about how the lattice method does not help students understand the place value in multiplication and it was just learning a procedure. However, Andy was ready for this, and showed a neat justification of why the lattice method works, by rotating a multiplication grid. The question to consider is, why don’t we let students use easier methods, as long as we keep it conceptually connected justifiying why they work? So my first takeaway – should we teach our year 7s the lattice method when they arrive, alongside why it works?
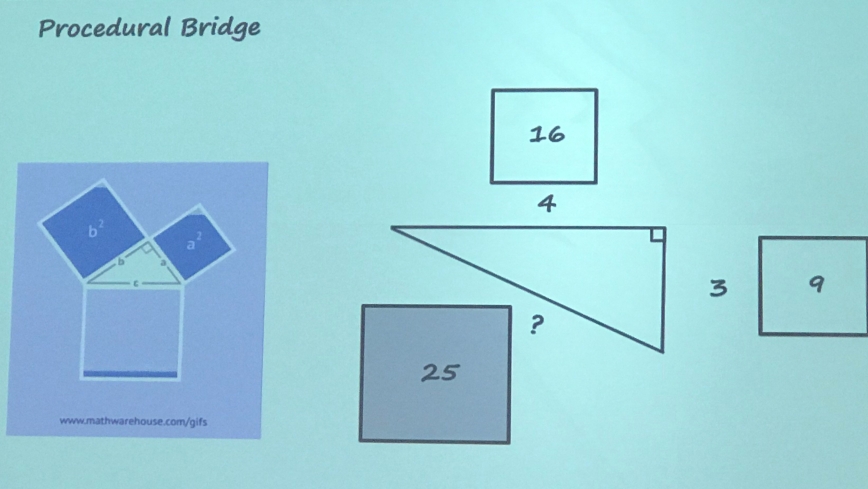The next idea was a game changer for Andy, and I love it! I wouldn’t even call it a procedure, but more making Pythagoras’ Theorem a bit more concrete, rather than the abstract algebra workings. I (and I’m sure many do) introduce Pythagoras looking at the square of the sides of the right angled triangle. Well why not draw squares next to each side and put the square value in?
We were now starting to get, on what Andy believed to be, more controversial ground. The DM method! And I’d agree, if it was introduced as a process with no understanding, it would be controversial. So what is it?! 
The DM method is basically a procedure to use for any maths that can be set up in proportional grids From ratios, to map scales, equivalent fractions to even inverse proportion.
And all it is is “divide, multiply”. But of course there is a justification – dividing establishes scale factor and multiplying applies the scale factor. This is definitely something that I want to explore.
The final idea we unfortunately didn’t get to explore as much as was possible in the workshop, but again is something I’d like to revisit, even if just for my interest. Andy has stopped starting trigonometry with SOHCAHTOA, but introducing trig using the Sine Rule.
Plenary Session – From Fermat to The Simpsons
How amazing to have Simon Singh, mathematician (background is mainly Physics), author, and one of the writers of The Simpsons to deliver a midday plenary session. Simon talked to us about some of his books: The Bible Code (and how for every prediction found in the Bible Code, one is also found in The Moby Dick Code!); Fermat’s Last Theorem; The Simpsons and their Mathematical Secrets (which I’ve read and enjoyed). It was a pleasure just to listen to Simon and his enthusiasm about his work.
Simon also mentioned some of the maths projects that he’s running for schools. For post 16s there is “Who wants to be a mathematician” – more can be found at http://goodthinkingsociety.org; and for KS4 Top-Top Set and Parallel https://parallel.org.uk, which is well worth an investigation.
Workshop 3 – Problem Solving
Claire took us on a tour of problem solving and some of the research around it. 
She looked at some of the definitions that have been given about problem solving and shared what what I thought was a great summary: challenging for individual learners; involves a strategy for solving that is not immediate or obvious and involve independent thought and creativity. Problem solving is another of my projects in our department, as we develop our SHAPED problem solving (taking the SHAPED genius of my HOD to implement it effectively to improve problem solving – hopefully more on this to come).
Claire looked at the why of problem solving and what we have to consider when problem solving with out students – some really useful considerations: cognitive load of the students; surface and deep structures (I really like the idea of trying to sort problems into similar groups, where there are multiple groups possible); growth mindset; generic problem solving skills (and whether there are any??!! but also identified the work of Polya’s 4 stages, which is what we’ve also used in our SHAPED problem solving) and topic specific problem solving skills.
Workshop 4 – Variation in mathematics
“Reflect, Expect, Check”
A treat of a workshop to finish, with Craig Barton, Jess Prior and Ben Gordon doing a triple act on how they’ve used variation theory in their teaching. Craig began, introducing 4 ways in which he uses variation theory: by example, by rule, by pattern and by demonstration. Then it was over to Jess to explain how she uses variation by example as an intelligent practice exercise. I love these!! I’ve started using them with some of my classes after reading Craig’s book, but without the full “reflect, expect, check” experience. However, they have already allowed questions and discussions about what is happening. The point is, instead of having unrelated practice questions, change one thing each time, so that the students have the opportunity to think about what’s changed and what effect this will have. At this point, it’s worth pointing out that from Craig’s point of view, this is one tool to use whilst giving student a wide diet of maths. I was so engrossed, I didn’t even get any pics! But Jess has very helpfully written in far more detail on her blog here at minimallydifferent.wordpress.com.
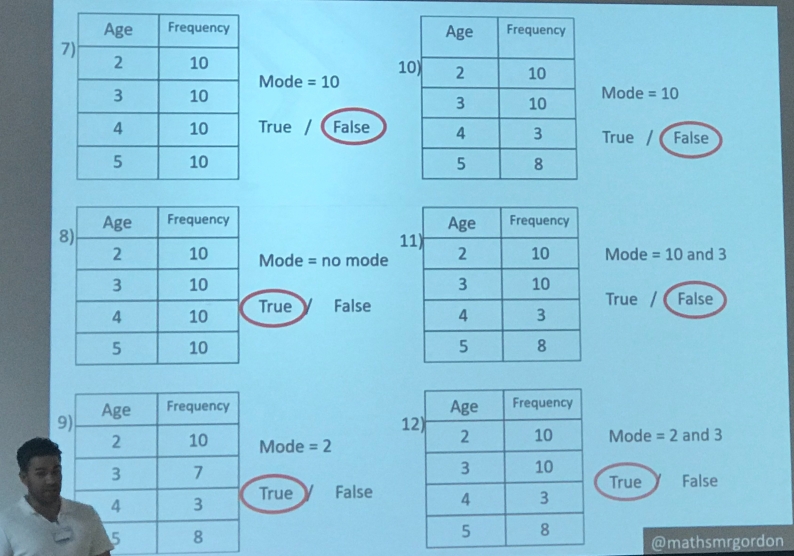Ben then took the baton to talk about variation by rule, and how he introduces concepts through examples and non-examples, but by varying one thing at a time in his examples. Again, I’ve done some of this, but not to the extent of only changing one thing! And it was hard to come up with the examples and non-examples as my list. Ben’s example of mode from a table was seamless, and his demonstrations of actually how to do it with the class were very useful. A silent introduction whilst students concentrate on the examples, cold calling for reasoning, insisting on correct language, and then class calling!
Both Jess and Ben came across as if they’d been hosting workshops to a packed lecture theatre alongside “famous” maths teachers for years, and not that it was their mathsconf debut! Craig then finished off with the other two variation methods, firstly making sure that if you are to use a pattern that to make sure it doesn’t become a pattern filling exercise, you leave a “gap of understanding” for students to identify the pattern, see what is happening, and use to predict the results. Finally with regards to variation by demonstration, the key point was to keep the initial diagram for a reference point. I really need to learn how to use geogabra!
Of course, Craig these days does not finish a workshop without an announcement, and true to form, there was an announcement at the end of this one. Craig, Jess and Ben have created a new website called variation theory.com. This will become a collaborative website with all things variation!
Final thoughts
If you haven’t been yet, you must go to a mathsconf. The CPD for maths teaching is amazing and the willingness to share in second to none. I was very excited to hear that mathsconf17 will be in my home town of Sutton Coldfield! Asking Mark whereabouts, he couldn’t remember but suggested I do a workshop. I had the intention before, but expressed how all that I know is what I’ve read about and heard about from other more expert people than me! Yet the kind Kris Boulton suggested to make that the basis of my workshop, as many other teachers won’t have read these, or heard about them. So, watch this space!
Danielle shared Alibali’s ideas for scaffolding, which reminds me not to always use the same method.
Initially I wasn’t going to go to Craig’s workshop. Not that I didn’t want to hear what he said, but more that I had already vacuumed up his book in a weekend of frenzied reading, and have listened to many of his podcasts with the experts from which Craig’s reading into the research had originated. How glad I am I changed my mind! Craig is a fantastic speaker and his depth of thought into maths teaching is inspiring. I have no problem in recommending any maths teacher, new or experienced, read Craig’s 
Intelligent practice is something else I am striving towards. At the moment, I attempt it rarely, but it is something that can become a powerful tool in students initial learning and understanding of a concept. Craig’s example with product of prime factors blew my mind! I thought it was genius how the questions develop so students can start to expect a certain answer, and then check it with their learning. And then every now and again a cognitive shock is thrown in when the answer isn’t what they expect and they look to see why, involving the hypercorrection affect (learning is more powerful when you are wrong about something you thought was correct).
Same structure, different deep problems (SSDD problems) were something else Craig introduced in his book and has since developed. These are problems which look the same, or are in the same context, but have different mathematical requirements for them, as on the example shown (this is one of mine!!). In this case they are different types of percentage questions, but the mathematical concepts in each question does not have to be related. Time for Craig’s second golden nugget – he has set up another website 
Then Matt introduced us to his favourite spreadsheet. Just a spreadsheet with cells coloured in red, green or blue, but when you zoom out it’s a picture of Matt! Here’s mine, created from Matt’s 
She gave some excellent phrases to use to support confidence and resilience, as well as ideas for resources that get pupils practising resilience in low entry challenges which can then be used as a starting point to praise the process of resilience. I would highly recommend Sarah’s workshop if she were to do another one.
From “tricks” for squaring n+0.5 two digit numbers, based on expanding brackets like earlier, to factor skyscrapers, HCF/LCM pyramids, the Ulan Sprial, Goldbach’s conjecture, happy numbers, Kaprekar’s routine, Sierpinksi triangle and Chaos Game to name a few, Johnny provided us with many ideas, with quite a few being being enable from his excellent 
Amir took his big 3 – Bloom’s Mastery, Englemann’s Direct Instruction and Cognitive Load Theory and looked at the common themes. He then boiled it down to Question, Model, Check, Praise and Retrieve. It is, of course, a bit more detailed than that! You can find Amir’s slides and handout 
For the classwork, I prepared a page, usually double sided, for each lesson, with the learning question already written on. I also decided to number the sheets with unit and lesson number on!
I was lucky that the notice boards were left with displays on, and that the classroom had been painted over the holidays, but I also wanted to make my own mark on the classroom, and put up displays that would both be useful and interesting. 
Ideas and resources have come from 
My absolute favourite part was finding out more about the Enigma machine, and I actually got to have a go on it too! It fascinates me both how it works and how the codes were broken. It was great to meet some more maths twitter folk (@arithmaticks, @mrsmathematica, @emmaemma53, @amercertbs and @travellingblue to name a few) as well as catch up with those I’ve met a few times (@rjs2212, @ejmaths, @solvemymaths). The quiz was, as always, hard but fun and I was kicking myself on the cryptarithm as I was just 2 numbers away from solving it but forgot about 0!!! My husband and boys met us for the evening meal as they were staying over too ready for a bank holiday day trip to Gullivers!!
The biggest thing we noticed was that in a good chunk of the samples, the teacher was working harder than the pupil, or the amount of teacher feedback compared to pupil response. We were doing our best to give quality feedback, but the resulting effort of the pupil was minimal and meant our feedback wasn’t doing it’s job in helping pupils improve. So as well as dealing with the pupils’ effort, we went on to discuss methods of giving concise and effective feedback. We discussed giving target or question codes, and then projecting the questions for each code for the pupils to complete, as suggested by @shaun_allison in his blog 
We then spent a chunk of time identifying the vectors that would move the points, and then shapes.
We finished the lesson with another Don Steward activiy, 
MathsZest 